Leetcode 287： Find the Duplicate Number

Description

Difficulty: Medium

Given an array nums containing n + 1 integers where each integer is between 1 and n (inclusive), prove that at least one duplicate number must exist. Assume that there is only one duplicate number, find the duplicate one.

Example:
Input: [1,3,4,2,2]
Output: 2

Note:

You must not modify the array (assume the array is read only).

You must use only constant, O(1) extra space.

Your runtime complexity should be less than O(n^2).

There is only one duplicate number in the array, but it could be repeated more than once.

找出数组里唯一的重复数字。
挑战点是如何压低运行的时间复杂度。

Solution - 1： Brute-force O(n^2)

基础思路：既然是压低复杂度，第一个想法是找能直接用的寻找方式，类似 nums.contains[id] ，但是这种方法无法剔除本身查找的数字，所以结果一直是true，（可行的方法是把数放进数字结构Set里，但是这样空间复杂度会过高，见Solution - 5）。

暴力解：遍历每一个数字的时候在剩下的数字里找是否有和当前数字相同的数，如果有，直接return。

class Solution {
    public int findDuplicate(int[] nums) {
        for(int i=0; i<nums.length;i++){
            for(int j=i+1; j<nums.length; j++){ // start to search from the next number
                if(nums[i] == nums[j]){
                    return nums[i];
                }
            }
        }
        return 0; //dummy return
    }
}

Space complexity : O(1)
Time complexity : O(n^2)

肯定不是最优解，果然…

Solution - 2： Sorting O(nlog(n))

思路：如果数列是按大小排列的，那么只需要确认相邻的两个数是否相同。

class Solution {
    public int findDuplicate(int[] nums) {
        Arrays.sort(nums); // sort the array
        for (int i = 1; i < nums.length; i++) {
            if (nums[i] == nums[i-1]) {
                return nums[i];
            }
        }
        return -1;
    }
}

Space complexity : O(1) or O(n)：如果可以用原本的数列（sort in place），即为O(1)，但是因为有第一条限制，所以这里是O(n)（其实违背了题目要求）。
Time complexity : O(nlog(n))：因为sort

Solution - 3： Binary Search O(nlog(n))

思路： 评论区一开始看到这个代码有点一头雾水，这不是只有在数列是按顺序排列的时候才成立嘛？后来发现这题目里很重要一点一直被我忽略了：。

Given an array nums containing n + 1 integers where each integer is between 1 and n (inclusive)

正常来说是有1-n个数，如果x是1-n里任意一个数，那么小于等于x的数的数量应该正好是x，即1-x。
现在因为有一个数重复，如果重复的数字小于等于x，那么小于等于x的数的数量就是x+1; 如果重复的数字大于x，那么小于等于x的数的数量就还是x。
因此我们可以一步步缩小范围来找到重复的数。这里虽然数字不是按大小排列的，但是它们的index是，所以范围left/right和中间值mid可以通过index来表示。这也是为什么Binary Search在这里行得通：

class Solution {
    public int findDuplicate(int[] nums) {
        int left = 1;
        int right = nums.length - 1;
        while (left <= right) { //!!!
            int mid = left + (right - left)/2;
            int count = 0;
            for (int a : nums) {
                if (a <= mid) ++count;
            }
            if (count <= mid) left = mid + 1;
            else right = mid - 1;
        }
        return left; //!!!
    }
}

Space complexity : O(1)
Time complexity : O(nlog(n))

**Solution - 4： Bit Manipulation O(n * 32)**

思路： 评论区很有意思的方法，利用了Integer有32 Bits来进行对比：

a：在整数1-n里，有多少数的第i个bit是1？
b：在数列nums里，有多少数的第i个bit是1？
如果b > a，那么结果res的第i个bit是1。

public int findDuplicate(int[] nums) {
    int n = nums.length-1, res = 0;
    for (int p = 0; p < 32; ++ p) {
        int bit = (1 << p), a = 0, b = 0;
        for (int i = 0; i <= n; ++ i) {
            if (i > 0 && (i & bit) > 0) ++a;
            if ((nums[i] & bit) > 0) ++b;
        }
        if (b > a) res += bit;
    }
    return res;
}

Space complexity : O(1)
Time complexity : O(n*32): 但是很有意思的是 nlog(n) < 32 所以这个方便并没有比前面两个更快。

Solution - 5： Set O(n)

思路： 我们可以把数放在一个数字结构Set里用于查找。在我们一个一个把数字加入前先在Set里查找是否已经有这个数存在，如果存在，可以直接return。

class Solution {
    public int findDuplicate(int[] nums) {
        Set<Integer> seen = new HashSet<Integer>();
        for (int num : nums) {
            if (seen.contains(num)) { // lookup num
                return num;
            }
            seen.add(num); // insert
        }
        return -1;
    }
}

Space complexity : O(n): 最糟糕的情况是相同的数位于第一个和最后一个，此情况下seen需要包含O(n-1)个数（其实违背了题目要求）。
Time complexity : O(n): 因为for循环（Set使用hash table，所以加入（add）和查找（contains）元素的时间都是固定的O(1)）

*Solution - 6： Floyd’s Tortoise and Hare (Cycle Detection) O(n)

思路： 我们使用函数f(x) = nums[x]来建立一个数列：x，nums[x]，nums[nums[x]]，nums[nums[nums[x]]]…即每一个数的位置是前一个数的值，如果我们从x =nums[0]开始，又因为nums里有一个重复的数字，这必将形成一个带有循环的数列，如下：

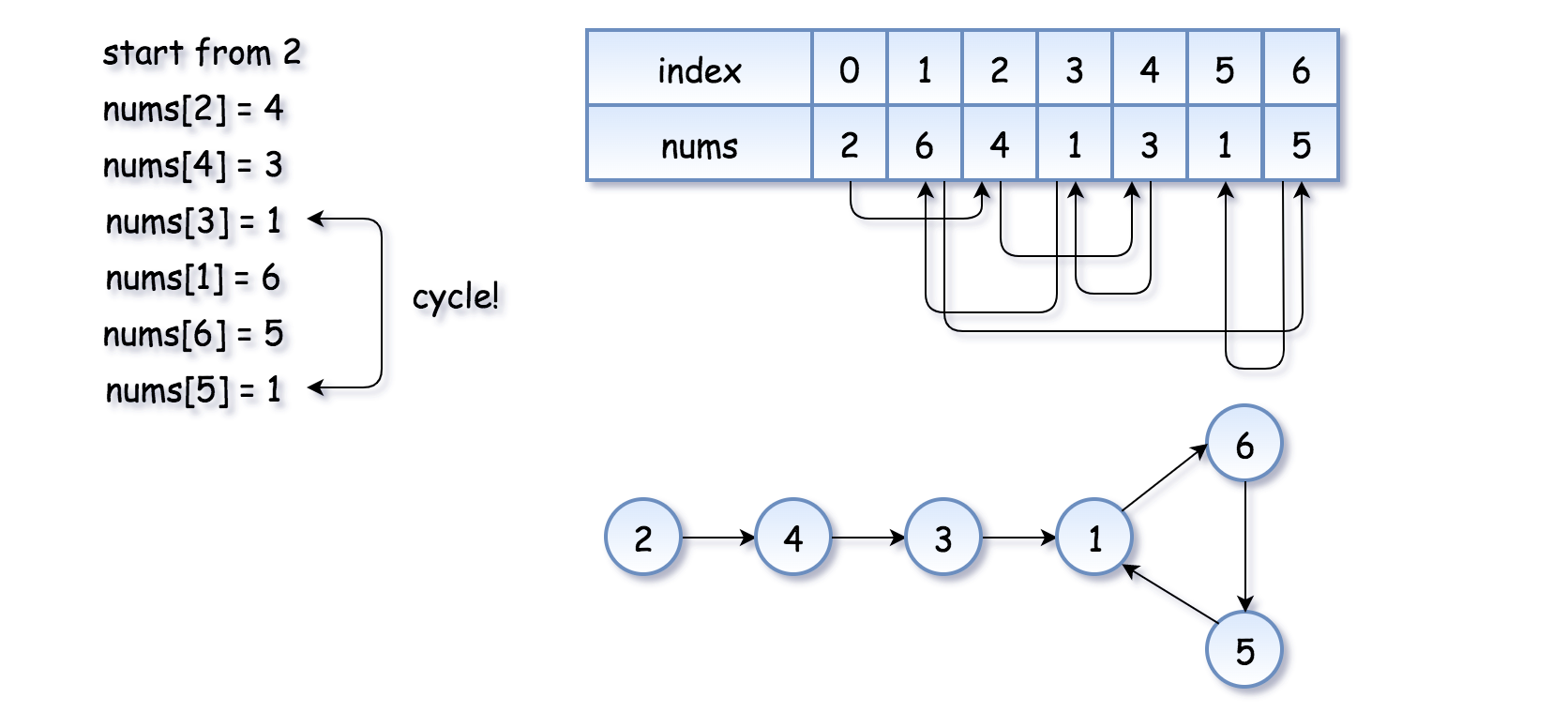
更复杂的例子 / 更大的圈：

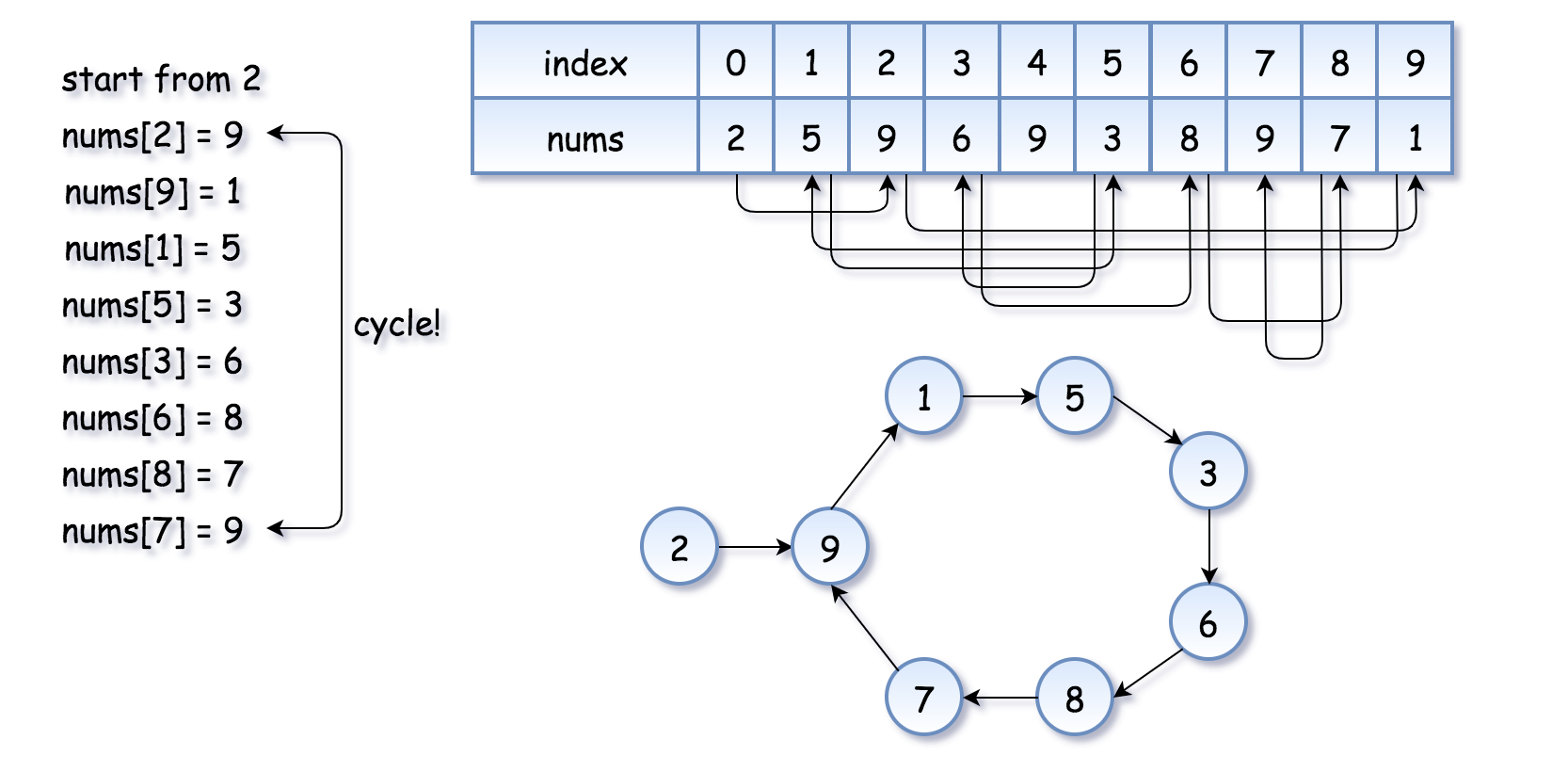
我们不难看出，进入循环的点就是我们要找的重复的数字（即例子里的1和9），问题是如何找到它？

Floyd’s algorithm：包含两个阶段和两个变量 tortoise（龟）和 hare（兔）。

阶段1：兔子的跳跃速度是乌龟爬行速度的两倍，即 hare = nums[nums[hare]], tortoise = nums[tortoise]。因为兔子的速度快，它会比乌龟更先进入循环，都进入循环后，在一个点兔子会和乌龟相遇。第一阶段结束，兔子胜利。
以第一个例子为准他们将相遇于点1：

兔子的路线为：2，3，6，1
乌龟的路线为：2，4，3，1

以第二个例子为准他们将相遇于点7：

兔子的路线为：2，1，3，8，9，5，6，7
乌龟的路线为：2，9，1，5，3，6，8，7

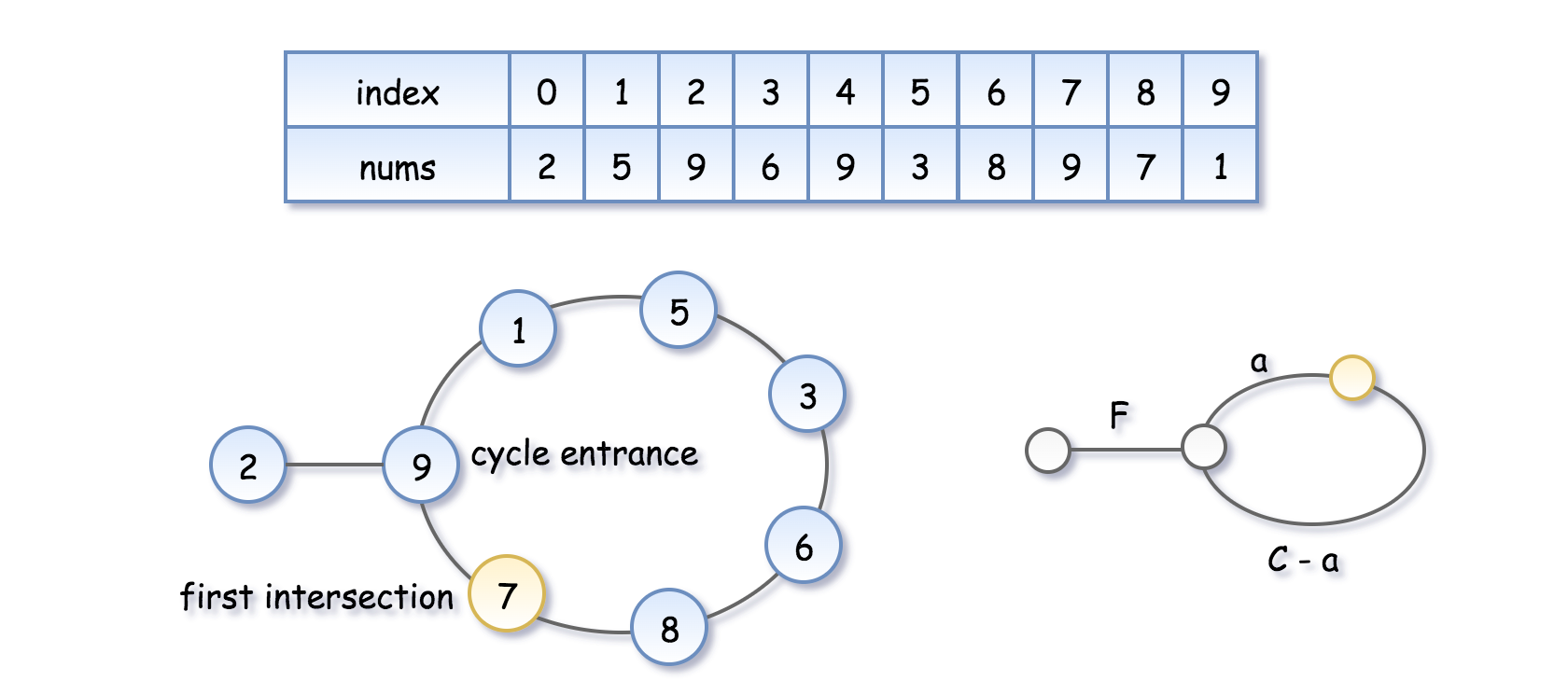
因为兔子的速度是乌龟的两倍，所用时间相同，兔子跑的距离也是乌龟的两倍：2d(tortoise) = d(hare)，设从起始点到进入循环点的距离为F，循环的长度为C，相遇点距离进入循环点的距离为a，则2(F+a) = F+nC+a，n为任意整数。因此我们可以得出F+a = nC。

阶段2：我们再给乌龟一次机会并把兔子的速度变成和乌龟一样，即hare = nums[hare], tortoise = nums[tortoise]。乌龟从起始点重新开始，而兔子从阶段1的相遇点开始。

以第一个例子为准他们将相遇于进入循环点1：

兔子的路线为：2，4，3，1
乌龟的路线为：1，5，6，1

以第二个例子为准他们将相遇于进入循环点9：

兔子的路线为：2，9
乌龟的路线为：7，9

为什么会这样呢？乌龟在F步之后会到达点F，而由于F = nC - a，兔子在F步之后也必定到达点F，所以这次兔子和乌龟会在进入循环的点相遇（即我们要找的重复的数）。

class Solution {
  public int findDuplicate(int[] nums) {
    // Phrase 1: Find the intersection point of the two runners.
    int tortoise = nums[0];
    int hare = nums[0];
    do {
      tortoise = nums[tortoise];
      hare = nums[nums[hare]];
    } while (tortoise != hare);
    
    // Phrase 2: Find the "entrance" to the cycle.
    tortoise = nums[0];
    while (tortoise != hare) {
      tortoise = nums[tortoise];
      hare = nums[hare];
    }
    return hare;
  }
}

Space complexity : O(1)
Time complexity : O(n)

Application

最后这道题现实中的应用和拓展：

Proving that at least one duplicate must exist in nums is simple application of the pigeonhole principle. Here, each number in nums is a “pigeon” and each distinct number that can appear in nums is a “pigeonhole”. Because there are n+1 numbers and n distinct possible numbers, the pigeonhole principle implies that at least one of the numbers is duplicated.

桌上有十个苹果，要把这十个苹果放到九个抽屉里，无论怎样放，我们会发现至少会有一个抽屉里面放不少于两个苹果。这一现象就是我们所说的“抽屉原理”。抽屉原理的一般含义为：“如果每个抽屉代表一个集合，每一个苹果就可以代表一个元素，假如有n+1个元素放到n个集合中去，其中必定有一个集合里至少有两个元素。” 抽屉原理有时也被称为鸽巢原理。

Summary

这道题本身并不难，但如何减少复杂度是一个难点，方法也是千奇百怪。
最后一个算法非常有意思，总觉得名字很眼熟，特地回去翻了一下发现之前学过一个叫Floyd-Warshall的算法，但这俩好像没啥关系…

总之希望自己能坚持下去，每周记录分享几道有趣的题和解法。也欢迎大家留言讨论补充(●’◡’●)