Bright's Blog

大达哒的小野望

0%

剑指offer 04： 二维数组中的查找 (Leetcode 240)

Posted on In , Valine:
Symbols count in article: 3.6k Reading time ≈ 3 mins.

Description

Difficulty: Simple

Write an efficient algorithm that searches for a value in an m x n matrix. This matrix has the following properties:

  • Integers in each row are sorted in ascending from left to right.
  • Integers in each column are sorted in ascending from top to bottom.

Example:

Consider the following matrix:

1
2
3
4
5
6
7
[
  [1,   4,  7, 11, 15],
  [2,   5,  8, 12, 19],
  [3,   6,  9, 16, 22],
  [10, 13, 14, 17, 24],
  [18, 21, 23, 26, 30]
]

Given target = 5, return true.

Given target = 20, return false.

二维数组中的查找，可以很方便地暴力解决，重点是如果利用此数组的特性更有效地解决问题。

Solution - 1： Brute-force O(n*m)

思路： 不考虑特性，正常的查找：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
         if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
            return false;
        }
        for(int i=0; i<matrix.length; i++){
            for(int j=0;j<matrix[0].length; j++){
                if(matrix[i][j] == target){
                    return true;
                }
            }
        }
        return false;
    }
}

Space complexity : O(1)
Time complexity : O(n*m)

Solution - 2： Binary Search O(mlog(n))

思路： 可以对每一行进行二分查找，如果每一行都没有查找到结果，就返回false。

  • 这里使用java库函数Arrays.binarySearch(matrix[i], target)，返回值非负说明查找到target。
  • 此外矩阵的每一列也是从小到大排列的，所以在对每一行进行二分查找的循环时，如果matrix[i][0] > target，这一行肯定没有指定元素，更下面的每一行的所有元素都大于matrix[i][0]也一定找不到指定元素，所以可以直接返回false。
1
2
3
4
5
6
7
8
9
10
11
public boolean searchMatrix(int[][] matrix, int target) {
        if (matrix == null || matrix.length == 0 || matrix[0].length == 0)
            return false;
        for (int i = 0; i < matrix.length; i++) {
            if (matrix[i][0] > target)
                return false;
            if (Arrays.binarySearch(matrix[i], target) >= 0)
                return true;
        }
        return false;
    }

Space complexity : O(1)
Time complexity : O(mlog(n)) m次for循环，每次binary Search的时间是log(n)

Solution - 3： 递归 O(n+m)

思路： 我们可以定义一个递归的查找函数

boolean search(int[][] matrix, int target, int left, int right, int top, int bottom)

表示在矩形区域[top, bottom]x[left, right]内是否存在target。

  • 如果left > right || top > bottom，则矩形区域不存在，return false。

  • 如果target < matrix[top][left] || target > matrix[bottom][right]，即矩形区域左上角元素大于target或者右下角的元素小于target，那也肯定无法在矩阵中找到该值，return false。

  • 通过 int mid = (left + right) / 2;搜索中间列是否能找到target，

    • 找到则直接return true
    • 找不到的话row会停在该列中间元素比target大的位置，再调用 search(matrix, target, left, mid - 1, row, bottom) || search(matrix, target, mid + 1, right, top, row - 1);如下图当我们确定 9<target<14时，可以判断 target一定在左下或者右上区域：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
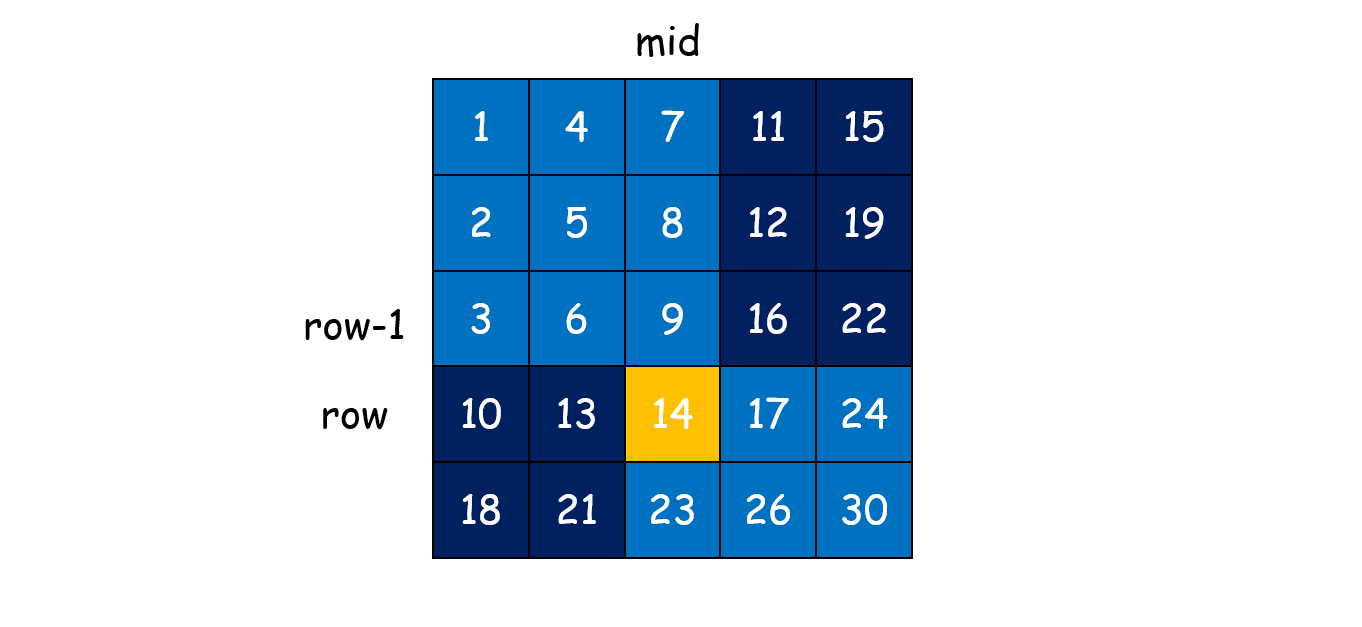
22
public boolean searchMatrix(int[][] matrix, int target) {
        if (matrix == null || matrix.length == 0)
            return false;
        return search(matrix, target, 0, matrix[0].length - 1, 0, matrix.length - 1);
    }

    private boolean search(int[][] matrix, int target, int left, int right, int top, int bottom) {
        if (left > right || top > bottom) 
            return false;
        if (target < matrix[top][left] || target > matrix[bottom][right])
            return false;
        
        int mid = (left + right) / 2;
        int row = top;
        while (row <= bottom && matrix[row][mid] <= target) { 
            if (matrix[row][mid] == target)
                return true;
            row++;
        }
        return search(matrix, target, left, mid - 1, row, bottom) ||
                search(matrix, target, mid + 1, right, top, row - 1);
    }

Space complexity : O(1)
Time complexity : O(mlog(n)) 因为最多row要加m次

Solution - 4： 线性查找 O(n+m)

思路： 由于给定的二维数组具备每行从左到右递增以及每列从上到下递增的特点，当访问到一个元素时，可以排除数组中的部分元素。

比如我们从二维数组的右上角开始查找（也可以从左下角出发，其他两个角不行）：

  • 如果当前元素等于目标值，则返回 true。
  • 如果当前元素大于目标值，则移到左边一列。
  • 如果当前元素小于目标值，则移到下边一行。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    public boolean findNumberIn2DArray(int[][] matrix, int target) {
        if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
            return false;
        }
        int rows = matrix.length, columns = matrix[0].length;
        int row = 0, column = columns - 1;
        while (row < rows && column >= 0) {
            int num = matrix[row][column];
            if (num == target) {
                return true;
            } else if (num > target) {
                column--;
            } else {
                row++;
            }
        }
        return false;
    }
}

Space complexity : O(1)
Time complexity : O(n+m)访问到的下标的行最多增加 n 次，列最多减少 m 次

Summary

  • 自己做的话真的只会暴力解决，但多点思路总是好的
  • 要善于利用数据的特点，比如最后一个解法就很完美。

总之希望自己能坚持下去，每周记录分享几道有趣的题和解法。也欢迎大家留言讨论补充(●’◡’●)

-------------End Thank you for reading-------------